Activation function

An activation function is a mathematical function that is applied to the output of a neuron in a neural network. The purpose of an activation function is to introduce non-linearity into the output of a neuron, allowing the neural network to learn more complex, non-linear relationships between inputs and outputs.

Activation functions allow neural networks to learn complex, non-linear relationships between inputs and outputs, which is essential for tasks such as image and speech recognition. Choosing the appropriate activation function depends on the specific problem and the characteristics of the data.

Feasibility condition for the activation function

The main conditions for an activation function in a neural network are:

Differentiability: The function must be differentiable so that the backpropagation algorithm can be used to compute gradients and update the model’s parameters.
Computational efficiency: The function should be computationally efficient to calculate as it will be applied to a large number of inputs during training and inference.
Output range: The output of the function should be within a reasonable range, this is important for the stability and performance of the network.
Non-Linearity: The function should introduce non-linearity to the network, this is crucial for the neural network to be able to learn complex relationships in the data.
Monotonicity: The function should be monotonically increasing or decreasing, this is to make sure that the gradient descent can find the global minimum.
Continuity: The function should be continuous, this is to make sure that the gradient descent can move smoothly to the global minimum.

Binary step function

Let us look at a simple function that can be used to create a binary classifier. A binary step function, also known as a Heaviside step function, is a type of activation function that maps all input values less than a certain threshold (usually 0) to 0 and all input values greater than or equal to the threshold to 1.

$f(x) =\begin{cases}1& \text{ if } x\geq 0\\0& \text{ if } x< 0\end{cases}$

Lets us see what the function looks like-

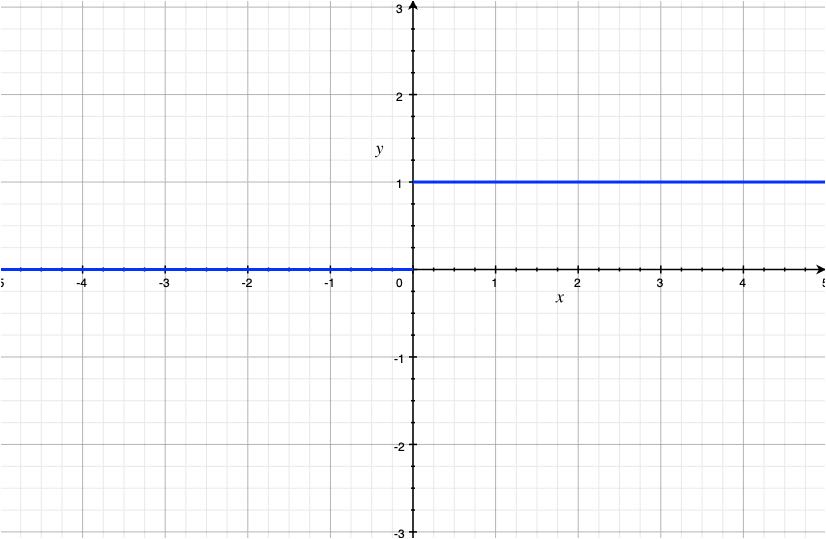
The drawback of this function is that its gradient step is 0 which causes hindrance in backpropagation.

Linear function

$f(x) = ax$

The linear activation function is a simple and computationally efficient function. However, when used as the sole activation function in a neural network, it can limit the network’s ability to learn more complex functions. This is because a linear function is not non-linear, and a neural network with only linear activation functions would be equivalent to a single-layer perceptron, which is a relatively simple model.

Therefore, the linear activation function is often used as an activation function in the output layer of a neural network, when the output is a continuous value. It can be also used as an activation function in an autoencoder, a type of neural network that learns to reconstruct input data.

Sigmoid

$f(x) = \frac{1}{1+e^{-x}}$

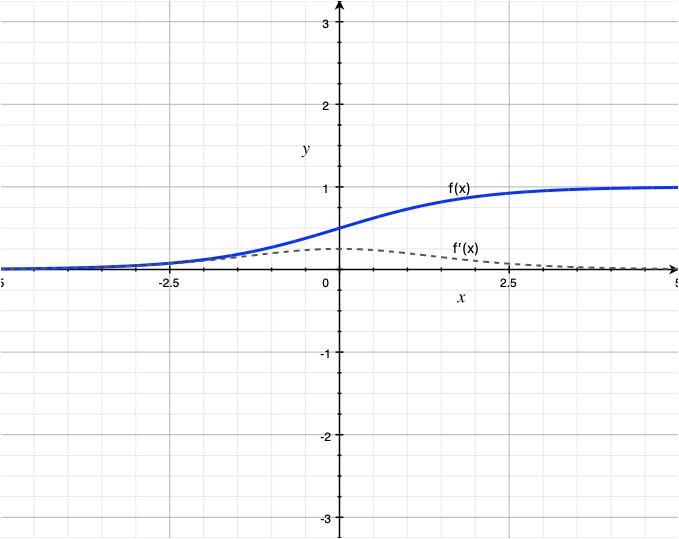
The sigmoid function is often used in the output layer of a binary classification neural network, where the output values correspond to the probability of the input belonging to one of the two classes. It is also used in the hidden layers of some networks.

One disadvantage of the sigmoid function is that it can saturate for large positive or negative input values, which means that the gradients can become very small and slow down or stop the training process which is called the Vanishing gradient. Another disadvantage is that its output is not zero-centered, making it harder to converge using certain optimization algorithms.

tanh – Hyperbolic tangent

$f(x) = 2 * sigmoid(2x) - 1$

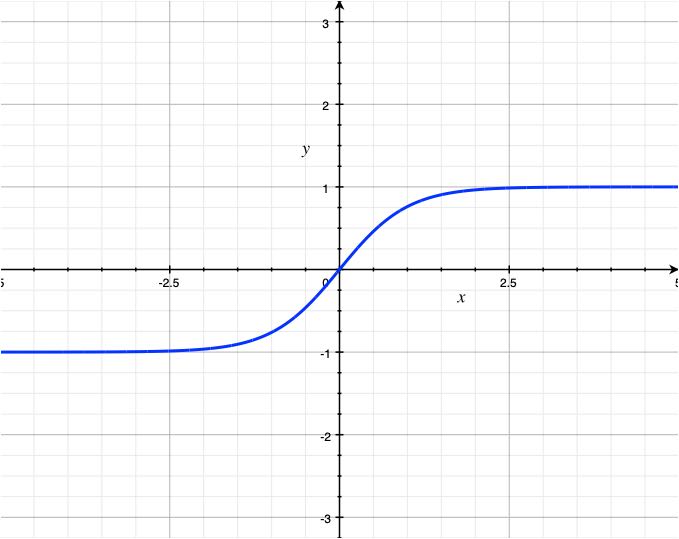
The tanh function is often used as the activation function in the hidden layers of a neural network. It is similar to the sigmoid function but its output is zero-centered, which makes it easier to converge using certain optimization algorithms.

One disadvantage of the tanh function is that it also can saturate for large positive or negative input values, which means that the gradients can become very small and slow down or stop the training process (Vanishing gradient).

ReLU – Rectified linear unit

$f(x) = max(0, x)$

ReLU is a linear function for positive values of x and it’s a constant function for negative values of x. The function returns the input x if it is positive, and 0 if it is negative. It has a slope of 1 for x > 0, and a slope of 0 for x <= 0. Therefore repeated multiplication with 1 gives the same number which addresses the vanishing gradient issue.

One disadvantage of the ReLU function is that it can produce “dead neurons” which happen when the input to the activation function is always negative, which means the output will always be zero. This can happen during the training process and make the network not able to learn from certain inputs. To overcome this problem, variants of ReLU such as Leaky-ReLU, PReLU, and ELU have been introduced.

Leaky ReLU

$f(x) =\begin{cases}x& \text{ if } x\geq 0\\a*x& \text{ if } x< 0\end{cases}$

where 0.01 <= a <= 0.1

This can help prevent the “dying ReLU” problem, where a neuron’s output is always 0, causing the neuron’s weights to never update during training. There are two more variants for similar use case.

Parameterized ReLU

$f(x) =\begin{cases}x& \text{ if } x\geq 0\\a*x& \text{ if } x< 0\end{cases}$

Exponential ReLU

$f(x) =\begin{cases}x& \text{ if } x\geq 0\\a(e^{x}-1)& \text{ if } x< 0\end{cases}$

Softmax

The softmax activation function is commonly used in the output layer of a neural network that is used for multi-class classification problems. It converts a set of input values into a probability distribution, where the sum of all output values is 1. The general form of the softmax function is:

$softmax(x_{i}) = \frac{e^{x_{i}}}{\sum_{j=1}^{n}e^{x_{j}}}$

The function maps the input values to a probability space, where each output value represents the probability of the input data belonging to the corresponding class. The class with the highest probability is chosen as the final output of the network.